Quando falamos de métodos quantitativos em finanças, uma das principais ferramentas conhecidas pelo mercado vem de uma elegante solução proposta no meio do século passado. Em seu artigo “Portfolio Selection”, publicado em 1952 no Journal of Finance, Harry Markowitz separa em duas etapas o processo de constituição de uma carteira de investimentos, sendo a primeira delas responsável pela atribuição de uma expectativa de performance para cada ativo em um universo disponível.
Da análise fundamentalista, em um extremo, até chegarmos na abordagem puramente quantitativa no outro, a diversidade de recursos disponíveis para executar tal tarefa se reflete na variabilidade de produtos que o mercado de capitais oferece, sendo a escolha da metodologia orientada pelos tipos de dados à disposição e habilidade do gestor do produto em utilizá-los da maneira correta. A partir das expectativas geradas, podemos selecionar uma parcela dos ativos analisados e realizar a distribuição de risco sobre eles, resultando na formação de um portfólio, objetivo da segunda etapa. É justamente nesta distribuição que Markowitz dá a sua contribuição para a literatura, ao formular, matematicamente, o processo decisório do investidor e solucioná-lo através do CLA¹.
Inicialmente, denominada por ele como “(E-V) rule” ², tal formulação nos dá, para um dado retorno esperado da carteira, a atribuição de pesos que resulta no menor risco possível, sendo risco definido como variância de seus retornos. O resultado se mostra consistente ao apresentar a desejável característica de diversificação ao evitar a concentração de risco em um único grupo de ativos muito semelhantes. Se repetido para uma série de expectativas de retorno, esse processo origina diversas carteiras com risco mínimo que, juntas, formam a conhecida fronteira de eficiência.
Um objeto de extrema importância na implementação do CLA é a matriz de correlação dos retornos do conjunto de ativos selecionados. Em termos simples, ela quantifica o grau de associação linear entre pares de ativos deste grupo. Como ilustração, observe a matriz de correlação abaixo:
Note que o universo, neste caso, é composto por algumas ações brasileiras pertencentes aos setores de energia, construção civil, financeiro e mineração/siderurgia. Empresas de mesmo setor, naturalmente, compartilham um comportamento semelhante no mercado, sendo cada um desses identificado por um bloco ao longo da diagonal secundária desta matriz. Mas, apesar deste alto grau de associação representar a intuição de um gestor de carteiras, ele é justamente uma fonte potencial de problemas para o CLA. O algoritmo utiliza a inversa da matriz de correlação que, neste contexto, está sujeita a erros numéricos pela limitação de precisão inerente dos computadores. Como consequência, temos a produção de soluções instáveis, que se traduz em alterações e custos desnecessários nas carteiras ao longo do tempo.
Apesar de pouco provável, podemos ter em mãos uma matriz que não terá esse tipo de problema, mas, para chegar a essa conclusão, precisamos de algum tipo de diagnóstico que pode ser feito ao olharmos para o número de condicionamento da matriz de correlação. O número de condicionamento é definido como a razão do maior autovalor da matriz pelo seu menor autovalor. E se o resultado não for significativamente maior do que 1, esse é o nosso dia de sorte. Caso contrário, precisamos tomar algumas providências. Dentre elas, há uma forma muito interessante de reduzir o número de condicionamento e trazê-lo para níveis mais aceitáveis ao retirar o ruído da nossa matriz. Isso pode ser feito com o auxílio da teoria de matrizes aleatórias e do teorema de Marchenko-Pastur, solução, claramente, exposta no livro Machine Learning for Asset Managers. Porém, mesmo com o tratamento, pode ser que o problema não seja resolvido.
Se por um lado isso gera uma frustração, por outro temos a oportunidade de explorar outros processos de construção pois, apesar de possivelmente ser a mais famosa, a formulação proposta por Markowitz não é a única existente. Métodos computacionalmente intensivos (e outros nem tanto) vêm ganhando espaço na indústria de gestão de ativos, porém grande parte deste mercado permanece se apoiando em técnicas clássicas por sua rastreabilidade (no sentido das operações que realizam) e na ilusão de que as alternativas são “black boxes”.
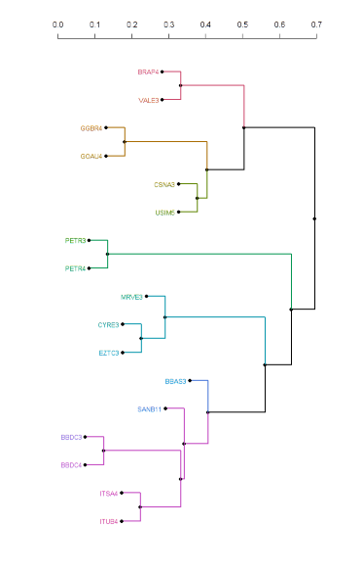
Se não quisermos abandonar, completamente, a matriz tratada anteriormente, podemos optar por um método hierárquico. Podemos definir em termos simples o conceito de hierarquia neste caso ao dizer que cada um dos elementos de um universo não pertence somente a um grupo, mas sim a diversos grupos que são encaixados um no outro. A figura anterior nos fornece uma dica da aplicabilidade dessa estrutura. Note que alguns blocos parecem fazer parte de outros ainda maiores, como é o caso da parcela formada por GGBR4 e GOAU4. Estas empresas formam um bloco menor entre si, mas também fazem parte de um bloco maior que sugere a dependência da commodity metálica. Apesar de uma inspeção visual parecer não fornecer mais sugestões (em um universo maior a identificação de todos os grupos seria uma tarefa praticamente impossível de ser concluída), tal estrutura não necessariamente para por aí. Para nossa sorte, este papel de busca fica em mãos de um algoritmo de agrupamento hierárquico. Um exemplo aplicado ao nosso universo em questão produz o seguinte resultado, onde o eixo à esquerda representa a distância entre cada nó encontrado pelo algoritmo:
Um artigo interessante que explora tanto o ponto fraco do método proposto por Markowitz e esta solução alternativa, é Building Diversified Portfolios That Outperform Out-Of-Sample, de Marcos López de Prado. Nesse artigo, o autor comenta a possibilidade de utilizar a estrutura de árvore na alocação top-down de risco, ao dividir a distribuição entre subconjuntos adjacentes de maneira inversamente proporcional às suas variâncias. Os resultados dos experimentos se mostram úteis para a solução do problema de instabilidade do CLA.
O tema de construção de portfólios tratado aqui chamou a atenção para apenas um dos possíveis passos no movimento de modernização das ferramentas quantitativas utilizadas na gestão de ativos. Métodos clássicos permanecem enraizados como principais componentes da caixa de ferramentas de muitos gestores, porém uma busca na literatura mais atual mostra já existirem alternativas que solucionam parte de problemas recorrentes dos métodos clássicos. Em uma indústria que carrega consigo grande responsabilidade como a de gestão de recursos de terceiros, essa modernização não deve ficar em segundo plano.
*Lucas Carboni, Analista Quantitativo na BV Asset
Referências
¹ CLA – Critical Line Algorithm
² (E,V) rule: Expected returns – variance of returns rule
Markowitz, Harry. “Portfolio Selection.” The Journal of Finance, vol. 7, no. 1, 1952, pp. 77–91. JSTOR, https://doi.org/10.2307/2975974.
López de Prado, Marcos and López de Prado, Marcos, Building Diversified Portfolios that Outperform Out-of-Sample (May 23, 2016). Journal of Portfolio Management, 2016; https://doi.org/10.3905/jpm.2016.42.4.059. ,Available at SSRN: https://ssrn.com/abstract=2708678 or http://dx.doi.org/10.2139/ssrn.2708678